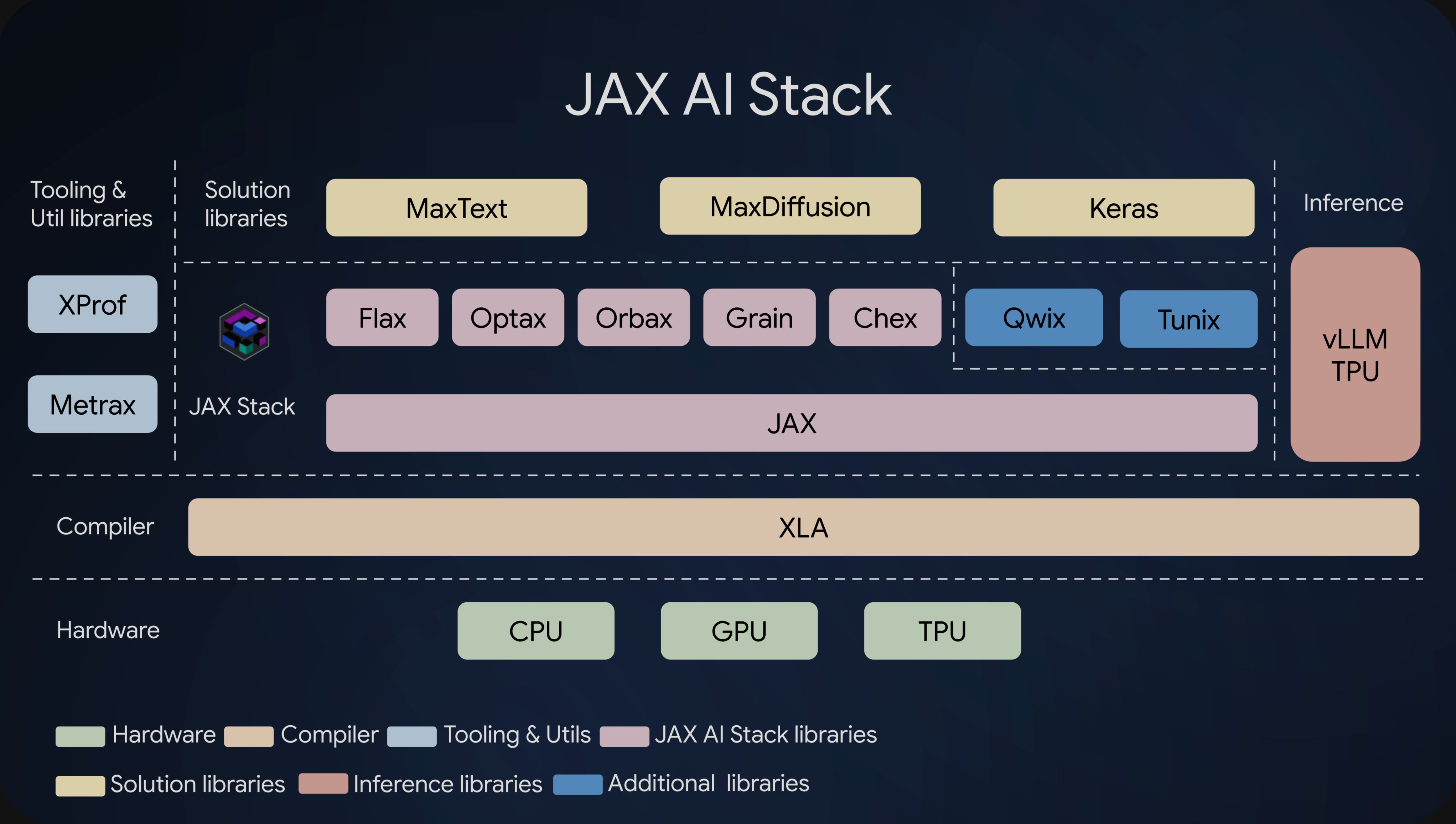
The JAX AI stack

Author

Marie-Hélène Burle

Content from the course slides for easier browsing.

What is JAX?

JAX is a high-performance accelerator-oriented array computing library for Python developed by Google. It allows composition, JIT-compilation, transformation, and automatic differentiation of numerical programs.

It provides NumPy-like and lower-level APIs.

It also requires strict functional programming.

Why JAX?

Fast

  • Default data type suited for deep learning

    Like PyTorch, uses float32 as default. This level of precision is suitable for deep learning and increases efficiency (by contrast, NumPy defaults to float64).

  • JIT compilation

  • The same code can run on CPUs or on accelerators (GPUs and TPUs)

  • XLA (Accelerated Linear Algebra) optimization

  • Asynchronous dispatch

  • Vectorization, data parallelism, and sharding

    All levels of shared and distributed memory parallelism are supported.

Great AD

01 Autodiff method 1 Static graph and XLA 02 Framework 2 Dynamic graph 1->2 a TensorFlow 4 Dynamic graph and XLA 2->4 b PyTorch 5 Pseudo-dynamic and XLA 4->5 d TensorFlow2 e JAX 03 Advantage 7 Mostly optimized AD 8 Convenient 9 Convenient 10 Convenient and mostly optimized AD 04 Disadvantage A Manual writing of IR B Limited AD optimization D Disappointing speed E Pure functions

summarized from a blog post by Chris Rackauckas

Close to the math

Considering the function f:

f = lambda x: x**3 + 2*x**2 - 3*x + 8

We can create a new function dfdx that computes the gradient of f w.r.t. x:

from jax import grad

dfdx = grad(f)

dfdx returns the derivatives:

print(dfdx(1.))
4.0

Forward and reverse modes

  • reverse-mode vector-Jacobian products: jax.vjp
  • forward-mode Jacobian-vector products: jax.jvp

Higher-order differentiation

With a single variable, the grad function calls can be nested:

d2fdx = grad(dfdx)   # function to compute 2nd order derivatives
d3fdx = grad(d2fdx)  # function to compute 3rd order derivatives
...

With several variables, you have to use the functions:

  • jax.jacfwd for forward-mode,
  • jax.jacrev for reverse-mode.

How does it work?

tracer Tracing jaxpr Jaxprs (JAX expressions) intermediate representation (IR) tracer->jaxpr jit Transformation hlo High-level optimized (HLO) program jit->hlo xla Accelerated Linear Algebra (XLA) CPU CPU xla->CPU GPU GPU xla->GPU TPU TPU xla->TPU transform Transformations py Pure Python functions py->tracer jaxpr->jit jaxpr->transform hlo->xla

tracer Tracing jaxpr Jaxprs (JAX expressions) intermediate representation (IR) tracer->jaxpr jit Just-in-time (JIT) compilation hlo High-level optimized (HLO) program jit->hlo xla Accelerated Linear Algebra (XLA) CPU CPU xla->CPU GPU GPU xla->GPU TPU TPU xla->TPU transform Vectorization Parallelization   Differentiation   py Pure Python functions py->tracer jaxpr->jit jaxpr->transform hlo->xla

tracer Tracing jaxpr Jaxprs (JAX expressions) intermediate representation (IR) tracer->jaxpr jit jax.jit hlo High-level optimized (HLO) program jit->hlo xla Accelerated Linear Algebra (XLA) CPU CPU xla->CPU GPU GPU xla->GPU TPU TPU xla->TPU transform jax.vmap jax.pmap jax.grad py Pure Python functions py->tracer jaxpr->jit jaxpr->transform hlo->xla

JAX for AI

Not itself a DL library

jx JAX dl Deep learning jx->dl op Optimizers jx->op pp Probabilistic programming jx->pp pm Probabilistic modeling jx->pm ll LLMs ll->jx so Solvers so->jx ph Physics simulations ph->jx

A sublanguage ideal for DL

jx JAX dl Deep learning jx->dl op Optimizers jx->op pp Probabilistic programming jx->pp pm Probabilistic modeling jx->pm ll LLMs ll->jx so Solvers so->jx ph Physics simulations ph->jx

The JAX AI stack

A modular approach:

noshadow

from the JAX AI Stack website