Sklearn workflow

Author

Marie-Hélène Burle

Scikit-learn has a very clean and consistent API, making it very easy to use: a similar workflow can be applied to most techniques. Let’s go over two examples.

This code was modified from Matthew Greenberg.

Load packages

from sklearn.datasets import fetch_california_housing, load_breast_cancer
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import (
    mean_squared_error,
    mean_absolute_percentage_error,
    accuracy_score
)

import pandas as pd

import matplotlib
from matplotlib import pyplot as plt

import numpy as np

from collections import Counter

Example 1: California housing dataset

Load and explore the data

cal_housing = fetch_california_housing()
type(cal_housing)

sklearn.utils._bunch.Bunch

Let’s look at the attributes of cal_housing:

dir(cal_housing)

['DESCR', 'data', 'feature_names', 'frame', 'target', 'target_names']

cal_housing.feature_names

['MedInc',
 'HouseAge',
 'AveRooms',
 'AveBedrms',
 'Population',
 'AveOccup',
 'Latitude',
 'Longitude']

print(cal_housing.DESCR)

.. _california_housing_dataset:

California Housing dataset
--------------------------

**Data Set Characteristics:**

:Number of Instances: 20640

:Number of Attributes: 8 numeric, predictive attributes and the target

:Attribute Information:
    - MedInc        median income in block group
    - HouseAge      median house age in block group
    - AveRooms      average number of rooms per household
    - AveBedrms     average number of bedrooms per household
    - Population    block group population
    - AveOccup      average number of household members
    - Latitude      block group latitude
    - Longitude     block group longitude

:Missing Attribute Values: None

This dataset was obtained from the StatLib repository.
https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html

The target variable is the median house value for California districts,
expressed in hundreds of thousands of dollars ($100,000).

This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).

A household is a group of people residing within a home. Since the average
number of rooms and bedrooms in this dataset are provided per household, these
columns may take surprisingly large values for block groups with few households
and many empty houses, such as vacation resorts.

It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.

.. rubric:: References

- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
  Statistics and Probability Letters, 33 (1997) 291-297

X = cal_housing.data
y = cal_housing.target

This can also be obtained with X, y = fetch_california_housing(return_X_y=True).

Let’s have a look at the shape of X and y:

X.shape

(20640, 8)

y.shape

(20640,)

While not at all necessary, we can turn this bunch object into a more familiar data frame to explore the data further:

cal_housing_df = pd.DataFrame(cal_housing.data, columns=cal_housing.feature_names)

cal_housing_df.head()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25

cal_housing_df.tail()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
20635	1.5603	25.0	5.045455	1.133333	845.0	2.560606	39.48	-121.09
20636	2.5568	18.0	6.114035	1.315789	356.0	3.122807	39.49	-121.21
20637	1.7000	17.0	5.205543	1.120092	1007.0	2.325635	39.43	-121.22
20638	1.8672	18.0	5.329513	1.171920	741.0	2.123209	39.43	-121.32
20639	2.3886	16.0	5.254717	1.162264	1387.0	2.616981	39.37	-121.24

cal_housing_df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 8 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      20640 non-null  float64
 1   HouseAge    20640 non-null  float64
 2   AveRooms    20640 non-null  float64
 3   AveBedrms   20640 non-null  float64
 4   Population  20640 non-null  float64
 5   AveOccup    20640 non-null  float64
 6   Latitude    20640 non-null  float64
 7   Longitude   20640 non-null  float64
dtypes: float64(8)
memory usage: 1.3 MB

cal_housing_df.describe()

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
count	20640.000000	20640.000000	20640.000000	20640.000000	20640.000000	20640.000000	20640.000000	20640.000000
mean	3.870671	28.639486	5.429000	1.096675	1425.476744	3.070655	35.631861	-119.569704
std	1.899822	12.585558	2.474173	0.473911	1132.462122	10.386050	2.135952	2.003532
min	0.499900	1.000000	0.846154	0.333333	3.000000	0.692308	32.540000	-124.350000
25%	2.563400	18.000000	4.440716	1.006079	787.000000	2.429741	33.930000	-121.800000
50%	3.534800	29.000000	5.229129	1.048780	1166.000000	2.818116	34.260000	-118.490000
75%	4.743250	37.000000	6.052381	1.099526	1725.000000	3.282261	37.710000	-118.010000
max	15.000100	52.000000	141.909091	34.066667	35682.000000	1243.333333	41.950000	-114.310000

We can even plot it:

plt.hist(y)

(array([ 877., 3612., 4099., 3771., 2799., 1769., 1239.,  752.,  479.,
        1243.]),
 array([0.14999 , 0.634992, 1.119994, 1.604996, 2.089998, 2.575   ,
        3.060002, 3.545004, 4.030006, 4.515008, 5.00001 ]),
 <BarContainer object of 10 artists>)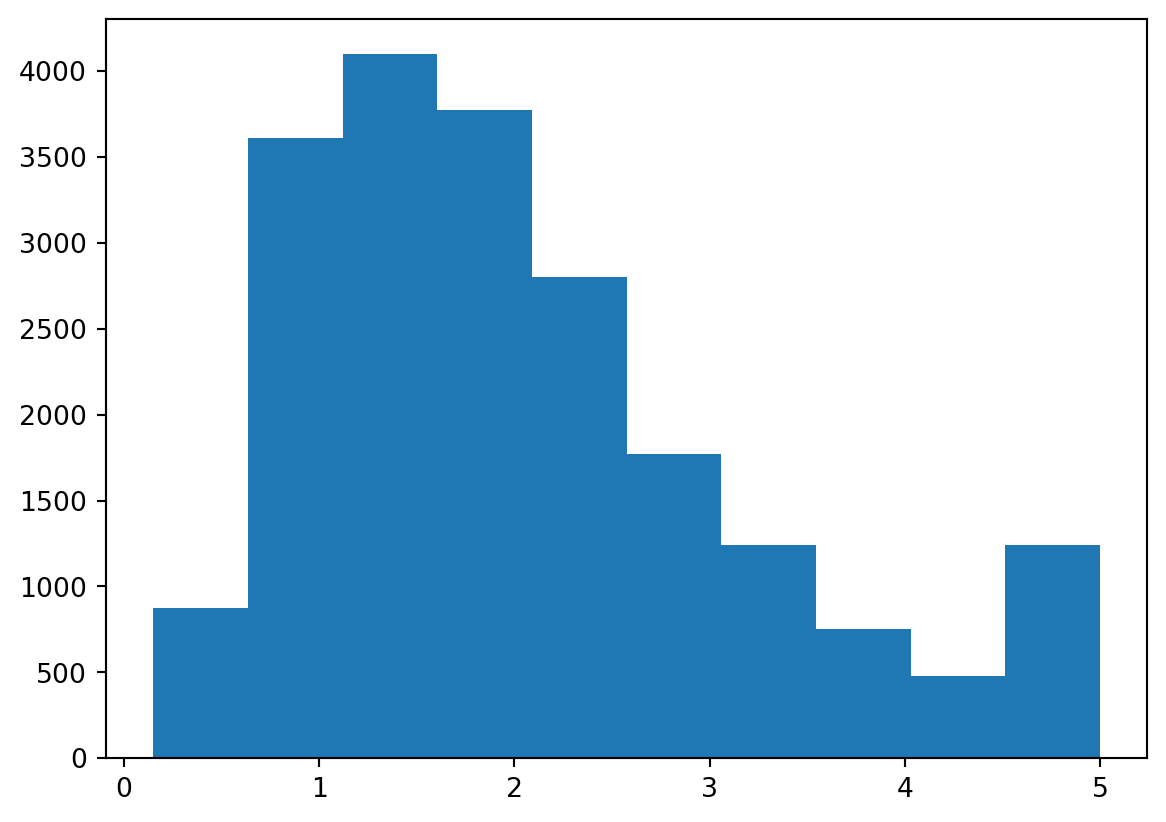

Create and fit a model

Let’s start with a very simple model: linear regression.

model = LinearRegression().fit(X, y)

This is equivalent to:

model = LinearRegression()
model.fit(X, y)

First, we create an instance of the class LinearRegression, then we call .fit() on it to fit the model.

model.coef_

array([ 4.36693293e-01,  9.43577803e-03, -1.07322041e-01,  6.45065694e-01,
       -3.97638942e-06, -3.78654265e-03, -4.21314378e-01, -4.34513755e-01])

Trailing underscores indicate that an attribute is estimated. .coef_ here is an estimated value.

model.coef_.shape

(8,)

model.intercept_

np.float64(-36.94192020718422)

We can now get our predictions:

y_hat = model.predict(X)

And calculate some measures of error:

Sum of squared errors

np.sum((y - y_hat) ** 2)

np.float64(10821.985154850292)

Mean squared error

mean_squared_error(y, y_hat)

0.5243209861846072

MSE could also be calculated with np.mean((y - y_hat)**2).

mean_absolute_percentage_error(y, y_hat)

0.31715404597233515

Index of minimum value:

model.coef_.argmin()

np.int64(7)

Index of maximum value:

model.coef_.argmax()

np.int64(3)

XX = np.concatenate([np.ones((len(X), 1)), X], axis=1)

beta = np.linalg.lstsq(XX, y, rcond=None)[0]
intercept_, *coef_ = beta

intercept_, model.intercept_

(np.float64(-36.94192020718429), np.float64(-36.94192020718422))

np.allclose(coef_, model.coef_)

True

This means that the two arrays are equal element-wise, within a certain tolerance.

X_test = np.random.normal(size=(10, X.shape[1]))
X_test.shape

(10, 8)

y_test = X_test @ coef_ + intercept_
y_test

array([-37.7624766 , -35.43989534, -37.62776124, -36.16743807,
       -36.70282941, -36.91231298, -36.84916   , -37.72509389,
       -35.90083768, -36.00753365])

model.predict(X_test)

array([-37.7624766 , -35.43989534, -37.62776124, -36.16743807,
       -36.70282941, -36.91231298, -36.84916   , -37.72509389,
       -35.90083768, -36.00753365])

Of course, instead of LinearRegression(), we could have used another model such as a random forest regressor (a meta estimator that fits a number of classifying decision trees on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting) for instance:

model = RandomForestRegressor().fit(X, y).predict(X_test)
model

array([1.4199201, 1.2526101, 1.5110801, 1.4515   , 1.5110801, 1.4446701,
       1.4515   , 1.5110801, 1.4479301, 1.1729801])

Which is equivalent to:

model = RandomForestRegressor()
model.fit(X, y).predict(X_test)

Example 2: breast cancer

Load and explore the data

b_cancer = load_breast_cancer()

Let’s print the description of this dataset:

print(b_cancer.DESCR)

.. _breast_cancer_dataset:

Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------

**Data Set Characteristics:**

:Number of Instances: 569

:Number of Attributes: 30 numeric, predictive attributes and the class

:Attribute Information:
    - radius (mean of distances from center to points on the perimeter)
    - texture (standard deviation of gray-scale values)
    - perimeter
    - area
    - smoothness (local variation in radius lengths)
    - compactness (perimeter^2 / area - 1.0)
    - concavity (severity of concave portions of the contour)
    - concave points (number of concave portions of the contour)
    - symmetry
    - fractal dimension ("coastline approximation" - 1)

    The mean, standard error, and "worst" or largest (mean of the three
    worst/largest values) of these features were computed for each image,
    resulting in 30 features.  For instance, field 0 is Mean Radius, field
    10 is Radius SE, field 20 is Worst Radius.

    - class:
            - WDBC-Malignant
            - WDBC-Benign

:Summary Statistics:

===================================== ====== ======
                                        Min    Max
===================================== ====== ======
radius (mean):                        6.981  28.11
texture (mean):                       9.71   39.28
perimeter (mean):                     43.79  188.5
area (mean):                          143.5  2501.0
smoothness (mean):                    0.053  0.163
compactness (mean):                   0.019  0.345
concavity (mean):                     0.0    0.427
concave points (mean):                0.0    0.201
symmetry (mean):                      0.106  0.304
fractal dimension (mean):             0.05   0.097
radius (standard error):              0.112  2.873
texture (standard error):             0.36   4.885
perimeter (standard error):           0.757  21.98
area (standard error):                6.802  542.2
smoothness (standard error):          0.002  0.031
compactness (standard error):         0.002  0.135
concavity (standard error):           0.0    0.396
concave points (standard error):      0.0    0.053
symmetry (standard error):            0.008  0.079
fractal dimension (standard error):   0.001  0.03
radius (worst):                       7.93   36.04
texture (worst):                      12.02  49.54
perimeter (worst):                    50.41  251.2
area (worst):                         185.2  4254.0
smoothness (worst):                   0.071  0.223
compactness (worst):                  0.027  1.058
concavity (worst):                    0.0    1.252
concave points (worst):               0.0    0.291
symmetry (worst):                     0.156  0.664
fractal dimension (worst):            0.055  0.208
===================================== ====== ======

:Missing Attribute Values: None

:Class Distribution: 212 - Malignant, 357 - Benign

:Creator:  Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian

:Donor: Nick Street

:Date: November, 1995

This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2

Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass.  They describe
characteristics of the cell nuclei present in the image.

Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree.  Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.

The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].

This database is also available through the UW CS ftp server:

ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/

.. dropdown:: References

  - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
    for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
    Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
    San Jose, CA, 1993.
  - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
    prognosis via linear programming. Operations Research, 43(4), pages 570-577,
    July-August 1995.
  - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
    to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
    163-171.

b_cancer.feature_names

array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
       'mean smoothness', 'mean compactness', 'mean concavity',
       'mean concave points', 'mean symmetry', 'mean fractal dimension',
       'radius error', 'texture error', 'perimeter error', 'area error',
       'smoothness error', 'compactness error', 'concavity error',
       'concave points error', 'symmetry error',
       'fractal dimension error', 'worst radius', 'worst texture',
       'worst perimeter', 'worst area', 'worst smoothness',
       'worst compactness', 'worst concavity', 'worst concave points',
       'worst symmetry', 'worst fractal dimension'], dtype='<U23')

b_cancer.target_names

array(['malignant', 'benign'], dtype='<U9')

X = b_cancer.data
y = b_cancer.target

Here again, we could have used instead X, y = load_breast_cancer(return_X_y=True).

X.shape

(569, 30)

y.shape

(569,)

set(y)

{np.int64(0), np.int64(1)}

Counter(y)

Counter({np.int64(1): 357, np.int64(0): 212})

Create and fit a first model

model = LogisticRegression(max_iter=10000)
y_hat = model.fit(X, y).predict(X)

Get some measure of accuracy:

accuracy_score(y, y_hat)

0.9578207381370826

This can also be obtained with:

np.mean(y_hat == y)

def sigmoid(x):
  return 1/(1 + np.exp(-x))

x = np.linspace(-10, 10, 100)
plt.plot(x, sigmoid(x), lw=3)
plt.title("The Sigmoid Function $\\sigma(x)$")

Text(0.5, 1.0, 'The Sigmoid Function $\\sigma(x)$')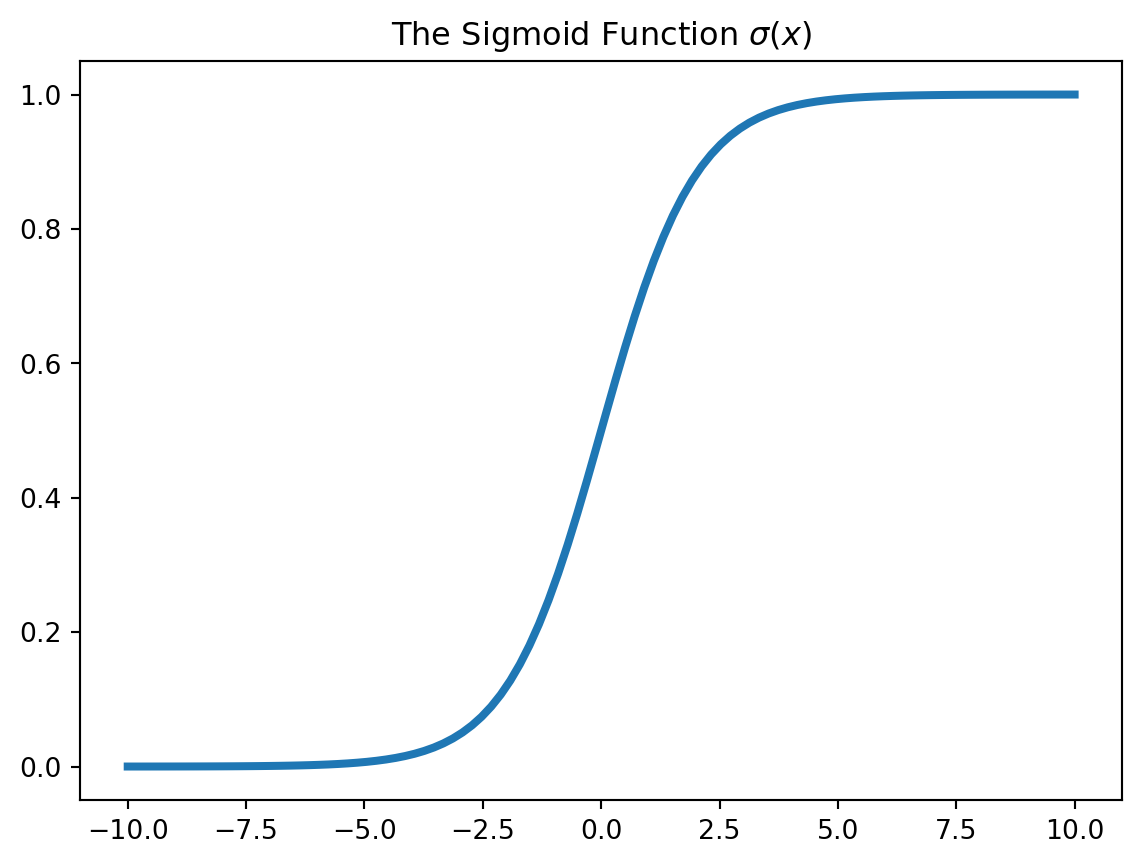

y_pred = 1*(sigmoid(X @ model.coef_.squeeze() + model.intercept_) > 0.5)
assert np.all(y_pred == model.predict(X))

np.allclose(
    model.predict_proba(X)[:, 1],
    sigmoid(X @ model.coef_.squeeze() + model.intercept_)
)

True

def make_spirals(k=20, s=1.0, n=2000):
    X = np.zeros((n, 2))
    y = np.round(np.random.uniform(size=n)).astype(int)
    r = np.random.uniform(size=n)*k*np.pi
    rr = r**0.5
    theta = rr + np.random.normal(loc=0, scale=s, size=n)
    theta[y == 1] = theta[y == 1] + np.pi
    X[:,0] = rr*np.cos(theta)
    X[:,1] = rr*np.sin(theta)
    return X, y

X, y = make_spirals()
cmap = matplotlib.colormaps["viridis"]

a = cmap(0)
a = [*a[:3], 0.3]
b = cmap(0.99)
b = [*b[:3], 0.3]

plt.figure(figsize=(7,7))
ax = plt.gca()
ax.set_aspect("equal")
ax.plot(X[y == 0, 0], X[y == 0, 1], 'o', color=a, ms=8, label="$y=0$")
ax.plot(X[y == 1, 0], X[y == 1, 1], 'o', color=b, ms=8, label="$y=1$")
plt.title("Spirals")
plt.legend()

Create and fit a second model

Here, we use a logistic regression:

model = LogisticRegression()
y_hat = model.fit(X, y).predict(X)
accuracy_score(y, y_hat)

0.5785

u = np.linspace(-8, 8, 100)
v = np.linspace(-8, 8, 100)
U, V = np.meshgrid(u, v)
UV = np.array([U.ravel(), V.ravel()]).T
U.shape, V.shape, UV.shape

((100, 100), (100, 100), (10000, 2))

np.ravel returns a contiguous flattened array.

W = model.predict(UV).reshape(U.shape)
W.shape

(100, 100)

plt.pcolormesh(U, V, W)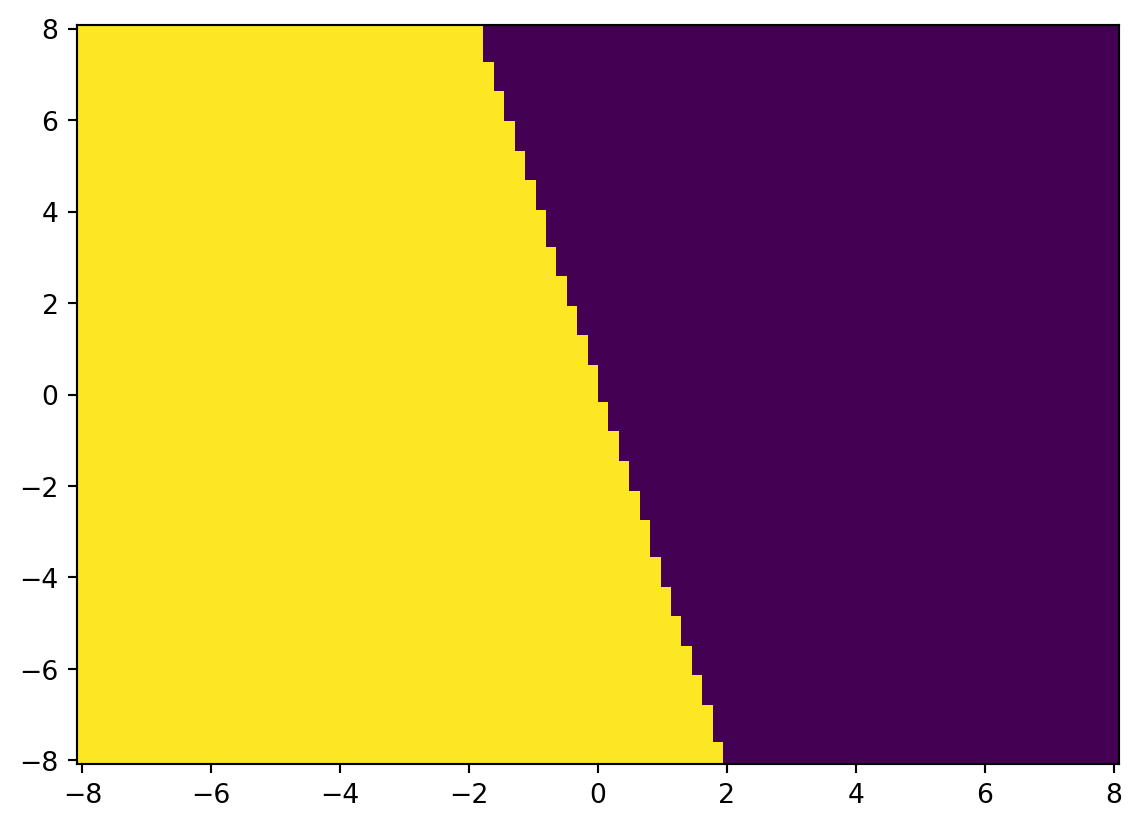

Create and fit a third model

Let’s use a k-nearest neighbours classifier this time:

model = KNeighborsClassifier(n_neighbors=5)
y_hat = model.fit(X, y).predict(X)
accuracy_score(y, y_hat)

0.8965

u = np.linspace(-8, 8, 100)
v = np.linspace(-8, 8, 100)
U, V = np.meshgrid(u, v)
UV = np.array([U.ravel(), V.ravel()]).T
U.shape, V.shape, UV.shape

((100, 100), (100, 100), (10000, 2))

W = model.predict(UV).reshape(U.shape)
W.shape

(100, 100)

plt.pcolormesh(U, V, W)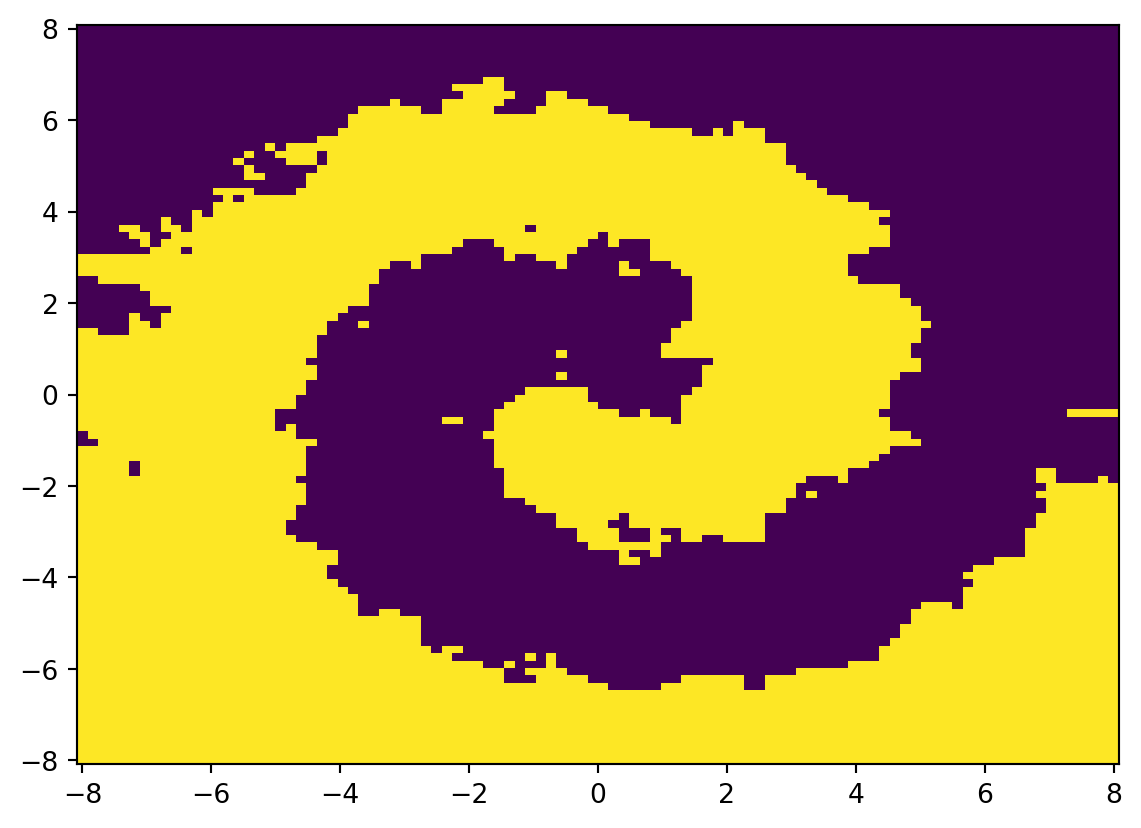

We can iterate over various values of k to see how the accuracy and pseudocolor plot evolve:

fig, axes = plt.subplots(2, 4, figsize=(9.8, 5))
fig.suptitle("Decision Regions")

u = np.linspace(-8, 8, 100)
v = np.linspace(-8, 8, 100)
U, V = np.meshgrid(u, v)
UV = np.array([U.ravel(), V.ravel()]).T

ks = np.arange(1, 16, 2)

for k, ax in zip(ks, axes.ravel()):
  model = KNeighborsClassifier(n_neighbors=k)
  model.fit(X, y)
  acc = accuracy_score(y, model.predict(X))
  W = model.predict(UV).reshape(U.shape)
  ax.imshow(W, origin="lower", cmap=cmap)
  ax.set_axis_off()
  ax.set_title(f"$k$={k}, acc={acc:.2f}")