Bayesian inference in JAX

Content from the webinar slides for easier browsing.

On probabilities

Two interpretations of probabilities

Frequentist

Image source

Bayesian

Image source

Frequentist

Frequentist approach to probabilities: assigns probabilities to the long-run frequency of events

It doesn’t assign probabilities to non-random variables such as hypotheses or parameters

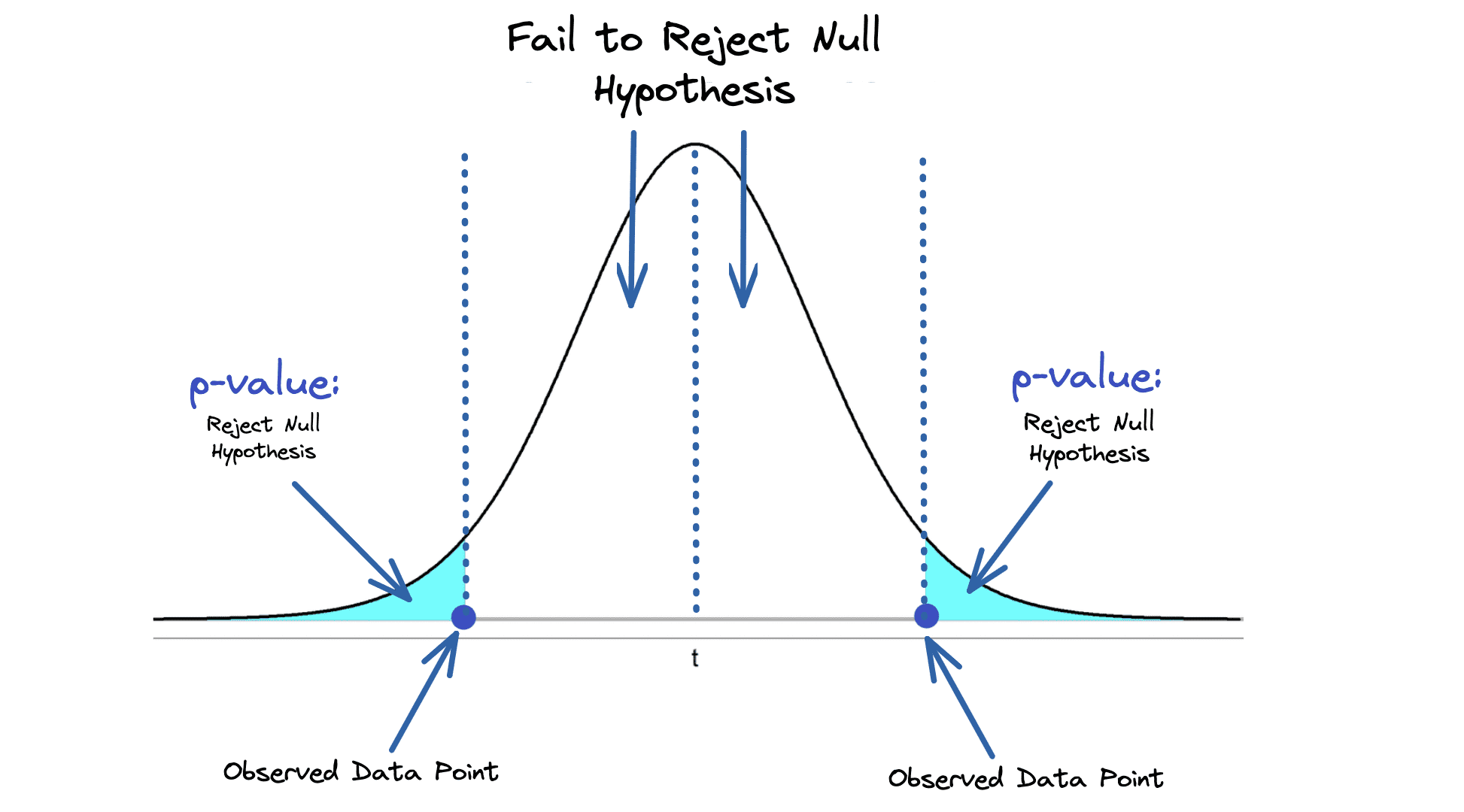
Instead, the probability is assigned to the limit of the relative frequencies of events in infinite trials and we can assign a probability to the fact that a new random sample would produce a confidence interval that contains the unknown parameter

This is not how we intuitively think and the results are hard to interpret. This approach is also often artificially constrained and limits the integration of various forms of information

It is however computationally simple and fast: samples are randomly selected from the sample space and it returns test statistics such as p-values and confidence intervals. This is why it was the dominant approach for a long time: we knew how to do it

Bayesian

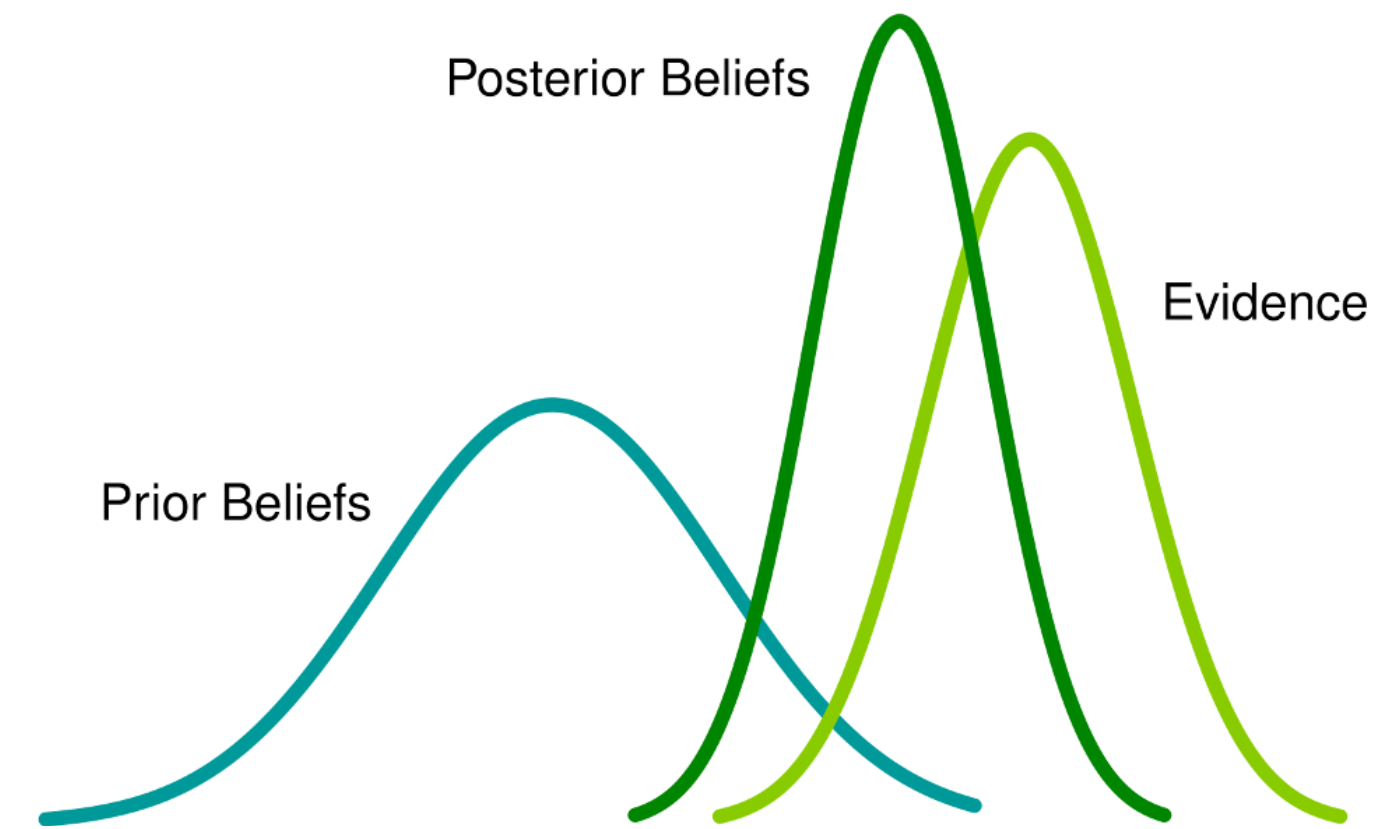
Bayesian approach: assigns probabilities to our beliefs about an event

Based on Bayes’ theorem of conditional probabilities which allows to calculate the probability of a cause given its effect:

$$P(A|X)=\frac{P(X|A)P(A)}{P(X)}$$

where:

• $P(A)$ is the prior probability of $A$—our belief about event $A$
• $P(X)$ is the marginal probability of event $X$ (some observed data)
• $P(X|A)$ is the likelihood or conditional probability of observing $X$ given $A$
• $P(A|X)$ is the posterior probability—our updated belief about $A$ given the data

Which approach to choose?

Bayesian statistics:

• is more intuitive to the way we think about the world (easier to interpret)
• allows for the incorporation of prior information and diverse data
• is more informative as it provides a measure of uncertainty (returns probabilities)
• is extremely valuable when there is little data (the inference is unstable and frequentist estimates have large variance and confidence intervals)

But beyond extremely simple examples, Bayesian inference is mathematically extremely arduous

It is also much more computationally heavy and only became possible to apply widely with the advent of powerful computers and new algorithms such as Markov chain Monte Carlo (MCMC)

Bayesian computing

Algorithms

A Bayesian approach to statistics often leads to posterior probability distributions that are too complex or too highly dimensional to be studied by analytical techniques

Markov chain Monte Carlo (MCMC) is a class of sampling algorithms which explore such distributions

Different algorithms move in different ways across the N-dimensional space of the parameters, accepting or rejecting each new position based on its adherence to the prior distribution and the data

The sequence of accepted positions constitute the traces

PPL

Probabilistic programming language (PPL), explained simply in this (a bit outdated) blog post, are computer languages specialized in creating probabilistic models and making inference

Model components are first-class primitives

They can be based on a general programming language (e.g. Python, Julia) or domain specific

First Bayesian PPLs

Relied on Gibbs sampling:

• WinBUGS replaced by OpenBUGS, written in Component Pascal
• JAGS, written in C++

BUGS = Bayesian inference Using Gibbs Sampling
JAGS = Just Another Gibbs Sampler

Stan

Stan (see also website and paper) is a domain-specific language

Stan scripts can be executed from R, Python, or the shell via RStan, PyStan, etc.

Also used as the backend for the R package brms which doesn’t require learning Stan but only works for simple models

Relies on No-U-Turn sampler (NUTS), a variant of Hamiltonian Monte Carlo (HMC) (see also HMC paper)

HMC and variants require burdensome calculations of derivatives. Stan solved that by creating its own reverse-mode automatic differentiation engine

Superior to Gibbs sampler ➔ made Stan a very popular PPL for years

PPLs based on DL frameworks

Since HMC and NUTS require autodiff, many Python PPLs have emerged in recent years, following the explosion of deep learning

Examples:

• Pyro based on PyTorch
• Edward, then Edward2 as well as TensorFlow Probability based on TensorFlow

Enters JAX

Had JAX existed when we started coding Stan in 2011, we would’ve used that rather than rolling our own autodiff system.

Bob Carpenter, one of Stan’s creators, in a recent blog post

What is JAX?

JAX is a library for Python that:

• makes use of the extremely performant XLA compiler
• runs on accelerators (GPUs/TPUs)
• provides automatic differentiation
• uses just-in-time compilation
• allows batching and parallelization

⇒ perfect tool for Bayesian statistics

See our introductory JAX course and webinar for more details

JAX idiosyncrasies

JAX is sublanguage of Python requiring pure functions instead of Python’s object-oriented style

It has other quirks

The only one you really need to understand for use in PPLs is the pseudorandom number generation

PRNG keys

Traditional pseudorandom number generators are based on nondeterministic state of the OS. This is slow and problematic for parallel executions

JAX relies on an explicitly-set random state called a key:

from jax import random
key = random.key(18)

Each key can only be used for one random function, but it can be split into new keys:

key, subkey = random.split(key)

The first key can’t be used anymore. We overwrote it with a new key to ensure we don’t accidentally reuse it

We can now use subkey in random functions in our code (and keep key to generate new subkeys as needed)

JAX use cases

New JAX backends

New JAX backends are getting added to many PPLs.

Edward2 and TensorFlow Probability can now use JAX as backend

PyMC relies on building a static graph. It is based on PyTensor which provides JAX compilation (PyTensor is a fork of aesara, itself a fork of Theano)

NumPyro

NumPyro is a library based on Pyro but using NumPy and JAX

Blackjax

Not a PPL but a library of MCMC samplers built on JAX

Can be used directly if you want to define your own log-probability density functions or can be used with several PPLs to define your model (make sure to translate it to a log-probability function)

Also provides building blocks for experimentation with new algorithms

Example Blackjax sampler: HMC

Example Blackjax sampler: NUTS

Which tool to choose?

All these tools are in active development (JAX was released and started shaking the field in 2018). Things are fast evolving. Reading blogs of main developers, posts on Hacker News, discourse forums, etc. helps to keep an eye on evolutions in the field

This recent conversation between Bob Carpenter (Stan core developer) and Ricardo Vieira (PyMC core developer) in the PyMC discourse forum is interesting

A lot of it also comes down to user preferences

Resources

Bayesian computing

Some good resources to get started with Bayesian computing:

• The book Probabilistic Programming & Bayesian Methods for Hackers by Cameron Davidson-Pilon provides a code-based (using PyMC) and math-free introduction to Bayesian methods for the real beginner
• Several resources on the PyMC website including intro Bayesian with PyMC
• NumPyro tutorials

More advanced: tutorials from Blackjax Sampling Book Project

From Stan to a JAX-based PPL

The code to the classic Bayesian textbook Statistical Rethinking by Richard McElreath got translated by various people to modern JAX-based PPLs and might help you transition from Stan: